PDF of this postI decided that upon finding Thomae's function, of which today's topic is about, that a good subsection of this journal of mathematical musings should be about what strange things can be mathematically correct, but not at all intended from a given definition. We look into the realm of real analysis today, a topic I am rather fond of, seeing as the real numbers are really more bizarre than one might originally think. Good old rational numbers, the collection of integer over natural (coprime), can approximate any real number to any arbitrary precision, yet the two fields are vastly different in mathematical properties.
That aside, which I might talk about in a later entry, I turn to the core discussion about continuous functions. How are they defined, and what's something really weird I can construct that is still considered continuous?
A function
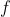
from a subset

to
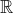
is said to be continuous at a point

if for every

, there exists a

such that if

and

, then

. Let us step back and get an intuitive understanding of this definition. If we look at

and all its neighbouring points, then we can get a neighbourhood in
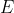
around
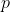
that all map into the neighbourhood about

. Visualising the

shrinking and the function still staying nicely mapped into the smaller and smaller neighbourhoods, this gives us a nice image about what it means to be continuous. Notice that this definition is for single points. If
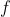
is continuous at all points

, then we say that the function is simply continuous. However, what if we construct a function that is continuous just about everywhere, and discontinuous everywhere else (which is also... everywhere?). Yes, I go back to my point about the rationals being able to approximate the reals to any arbitrary precision - in other words, dense in
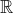
. Thomae's function is continuous at every irrational point, and discontinuous at every rational point. Thomae's function is defined as

if
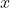
is irrational,

if

, and if

we say

. Let us first prove that
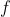
is discontinuous at each rational point. Let

be arbitrary, let

, and let

be arbitrary. Since the irrationals are dense in
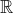
, there exists an

such that

. Since

and

,

. Thus since

was arbitrary, for all

there exists an

such that

implies

. By the definition of discontinuous,
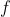
is discontinuous at

. Since

was arbitrary,
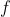
is discontinuous at every rational point.
Next we show the more shocking result that
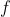
is continuous on an arbitrary irrational
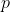
. Let

be arbitrary. By the Archimedean property, there exists an

such that

, so

. Call the set of rationals with denominator at most
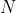
within

set
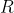
. We know that

is finite from the following combinatorial argument. Since

and

, the number of rationals with denominator
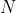
in the desired range is less than or equal

, and so forth for natural numbers

, so

is finite. Let

. There are two cases for

such that

, where
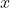
is irrational and thus

, or

where

and

. In this case,
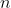
cannot be less than
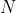
since
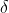
is defined to be small enough to skip each point in

with a smaller denominator than
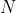
. Thus

, so

. Therefore
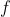
is continuous at
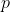
. For more information and an image of what
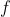
looks like, take a look at
the Wikipedia page.