Post inspired by: The Last Denominator
I just want to let people know that there is no way that any (true) theorem about the field of real numbers (or any field) has a division by zero. In order to get to the concluding statement would require an element that is 1/0 (which I will call the inverse of zero) to be summoned. Since this element does not exist in a field other than the zero ring (in which case 0 = 1), it cannot be used. The step taken is invalid.
Now that I have shown that the usage of zero's inverse is invalid, I will show that no true statement can imply a theorem that involves zero's inverse. By the axioms of inference that logicians, philosophers and mathematicians have developed, A implies B is equivalent to (NOT A) OR B. Therefore since B = conclusion with zero's inverse, if A is true, then the implication is false. And so we conclude that only false statements can imply the existence of zero's inverse (with the exception of the extremely uninteresting case of the zero ring).
To those of you who do not know to what I refer to as a ring and field, here is the break down (first we need the concept of a group):
A group G is a set of elements with a very limited amount of structure imposed on them under one operation (call it *):
1) There exists an identity element, 1, such that 1*x = x for each element x in G.
2) There exists an inverse element 1/x such that 1/x * x = 1 for each x in G.
3) For two elements in G, x and y, x*y is also in G.
4) For three elements in G, x,y and z, (x*y)*z = x*(y*z). In other words, * is an associative operation.
A ring R is simply a set of elements that have a certain structure under two operations defined among the elements (call them + and *):
1) R is an abelian group under + (abelian just means that for x,y in R, x + y = y + x. In other words, + is commutative).
2) For two elements x, y in R, x*y is in R.
3) The distributive laws hold: x,y,z in R imply x(y + z) = xy + xz, and (x + y)z = xz + yz.
A field F is a special kind of ring that really has a lot of great qualities that allow us to prove a lot of cool things:
1) F is a ring.
2) All elements of F except the identity of + form an abelian group under *.
The "except the identity of +" is the key term. Since we commonly call the identity of +, 0, this means that 0 is not required to have an inverse (with regards to *) in F. We know that the real numbers form a field because every element other than 0 has a multiplicative inverse (namely 1/x), and every element has an additive inverse (-x), and you can't add or multiply two numbers and get an answer that isn't a real number. Since 0*x = 0 for any x in the reals, 0 does not have an inverse z such that 0*z = 1. Thus 0 does not have an inverse in the real numbers.
Okay? Now you can be sure that if you get a division by 0 that either the number is too small for your calculator to keep the correct precision and it just rounded to 0, you started off with a false statement, or you had an incorrect deductive step.
Friday, December 5, 2008
Tuesday, November 25, 2008
The intersection inference problem is NP-complete
PDF for this post
First let me start off by defining the intersection inference problem.
Given a set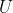 , some finite number (
, some finite number ( ) subsets
) subsets  , and
, and 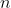 constants
constants  , is there a subset
, is there a subset  such that
such that  for
for 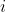 ranging all
ranging all 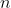 values?
values?
First we prove that intersection inference is in NP. Suppose we have a solution . In order to verify that
. In order to verify that 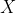 is indeed a solution, we perform the
is indeed a solution, we perform the 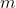 intersections of
intersections of 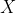 with
with 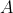 and confirm that
and confirm that  . Set intersection can be performed (naively) in
. Set intersection can be performed (naively) in  time, so this process is indeed polynomial and clearly yields the correct answer. Thus intersection inference is in NP.
time, so this process is indeed polynomial and clearly yields the correct answer. Thus intersection inference is in NP.
To prove intersection inference is NP-complete, we will show a reduction from 3-dimensional mapping to the intersection inference problem. With an arbitrary instance of the 3-dimensional mapping problem defined as sets such that
such that  ,
,  and
and  . To reduce this to the intersection inference problem, let
. To reduce this to the intersection inference problem, let  , and define
, and define  to be the subsets of triples that contain
to be the subsets of triples that contain  respectively. Define in a similar manner from
respectively. Define in a similar manner from 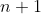 to
to 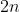 for
for  and from
and from  to
to  for
for  . Finally define
. Finally define  . The constraints are
. The constraints are  and
and  for
for  . We can see that to create these subsets takes
. We can see that to create these subsets takes  time in the rather straightforward manner of iterating over
time in the rather straightforward manner of iterating over 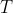 's elements to divvy up the elements into arrays representing
's elements to divvy up the elements into arrays representing  .
.
Through this construction we can see that exactly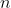 triples must match, and only one triple can contain each specific element in
triples must match, and only one triple can contain each specific element in  . Thus if there exists a solution to this intersection inference problem, the solution is exactly the
. Thus if there exists a solution to this intersection inference problem, the solution is exactly the 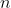 triples that satisfy the 3-dimensional matching problem. If there does not exist a solution, then at least one constraint was not satisfied, meaning at least one element in
triples that satisfy the 3-dimensional matching problem. If there does not exist a solution, then at least one constraint was not satisfied, meaning at least one element in  was not covered, or all elements were covered with some redundancies. Thus the reduction is correct and intersection inference is NP-complete because a known NP-complete problem was poly-time reducible to the intersection inference problem which is in NP.
was not covered, or all elements were covered with some redundancies. Thus the reduction is correct and intersection inference is NP-complete because a known NP-complete problem was poly-time reducible to the intersection inference problem which is in NP.
First let me start off by defining the intersection inference problem.
Given a set
First we prove that intersection inference is in NP. Suppose we have a solution
To prove intersection inference is NP-complete, we will show a reduction from 3-dimensional mapping to the intersection inference problem. With an arbitrary instance of the 3-dimensional mapping problem defined as sets
Through this construction we can see that exactly
Thursday, August 7, 2008
Windows installer and bad design
So I have a hard drive that I use to share data between my Linux and Windows OSes. That drive is in EXT2 and thus does not support the "hidden" file attribute. I decided I wanted to install Visual Studio Express 2008, but behold... the installer decides to use my EXT2 drive to extract to and then copy from into my temp directory on the other hard drive. Ridiculous? I haven't even started yet.
Setup decided to create a file called $shtdwn$.req with the hidden bit on. During the copy process, instead of saying, "these are the files I need. Copy them," it just gets the directory contents and tries to copy them all. This would work on any file system that supports the hidden attribute. The kicker? Well, first of all I have no idea why it decided to use P: instead of C:, but more importantly I could not discover any way to reconfigure this setting. No command-line argument help prompt in order to discover said functionality... I even tried using the cmd prompt to copy at elevated privileges to no avail.
But to my relief, the gurus of Linux prevail (yes, not a windows dev... hah) and give me a workaround.
set _SFX_CAB_SHUTDOWN_REQUEST=$shtdwn$.req
before running vcssetup.exe and it will skip that file. I'm pretty sure it just has to contain a value and not $shtdwn$.req specifically, but I didn't bother to test.
This post is for people like me in the future. For those of you that stumble upon this page, I hope this is what you were looking for.
Setup decided to create a file called $shtdwn$.req with the hidden bit on. During the copy process, instead of saying, "these are the files I need. Copy them," it just gets the directory contents and tries to copy them all. This would work on any file system that supports the hidden attribute. The kicker? Well, first of all I have no idea why it decided to use P: instead of C:, but more importantly I could not discover any way to reconfigure this setting. No command-line argument help prompt in order to discover said functionality... I even tried using the cmd prompt to copy at elevated privileges to no avail.
But to my relief, the gurus of Linux prevail (yes, not a windows dev... hah) and give me a workaround.
set _SFX_CAB_SHUTDOWN_REQUEST=$shtdwn$.req
before running vcssetup.exe and it will skip that file. I'm pretty sure it just has to contain a value and not $shtdwn$.req specifically, but I didn't bother to test.
This post is for people like me in the future. For those of you that stumble upon this page, I hope this is what you were looking for.
Wednesday, July 23, 2008
BrowserOS
This somewhat unorganized post is about my vision of desktops merging with the internet. A day's brainstorm session, let's say.
Abstract
An amazing amount of our time is spent online. So much so that browsing the web has become more natural to us than browsing our computer. My vision of computers in the future (apart from Minority Report-style holographic and surface computing) involves intertwining the browser and the rest of the computer. What I see involves probably the biggest risk toward this approach, and that is getting rid of hierarchical directories to store files, but rather allowing a user to search for documents via a common search engine query.
The File System (BrowserFS)
Files can be tagged by users and also by a background data mining process for relevancy determining algorithms. The way to best implement this is to have one's hard drive be totally a one- to two-level database system.
What is a two-level database system? Well, in my mind there are three types of files. User-created/owned, executable, and application data. Application data would be stored in the second level of the database. The second level is a database as a blob entry in the first level of the database in order to minimize clutter and narrow query results to relevant areas. The motivation for this, or rather my inspiration for this comes from my observation of two classes of applications. One class uses many flat files in complex directory hierarchies, and the other uses very few "packed" files which are basically virtual file systems that have all those many flat files organized as described of the previous class. Obviously one approach is cleaner than the other, and there only exists one level of indirection between the two. If the OS API has a boolean in fopen, say, that specifies if the data is first or second level, the resulting query could be limited to the application database.
"But wait!" you say, "Applications don't need to search for their data files, since they know exactly what they need. Don't introduce this overhead." I agree 100%, which brings me to my next idea.
The development tools for this operating system would allow order to be introduced to files residing on the build system. A tool that could create directory hierarchies that references files residing on the system would output a necessary build file for dependent data files. We impose directory hierarchies because hey, we know that's how we organize without ad hoc search queries. The most important reason however is because creating a URI to the file would allow direct access without queries. Since before shipping an application, one generally works in debug mode, debug applications would use this hierarchy file to open the referenced files on the first level database. Ship applications however would compile the second level database BLOB and work as described.
Applications can still access all other files; first or second level. The second level database is just another file in the first level database, only access to it is optimized more in the OS kernel. Thus if a user specifies he wants to use that application database file that a search has given him, he can, and then browse though that database as well. This is all if he has the permissions to do so, of course.
So where are the first level files, and how do applications access them once search spits them out? Well they all have URIs too, and querying the database in standard fashion can output all files on your computer if one so desires. The main difference is that first-level file URIs are assigned by the OS, and the second-level file URIs are assigned by the developer.
File Name and Extension Makeover
File names and file extensions are no longer what you might think either. A file extension is an attribute of a file record in the database that will either reference an application (applications register extensions with the OS by simply being applications on the system) that will open it, or are generic (ex. type EXT) and do not reference an application. So developers can still change a file's type, and it's still by changing what filename.end ends with, but by changing the extension, a disambiguation text extension would ask if it's for common applications A, B, C, Generic, or search. With machine learning, the OS can determine the behavior it should take by default for changing certain file names to others.
Keep in mind file names are no longer file names. They're optional titles that are also part of the user tags (weighted differently though) that are displayed on search results, along with snippets, if enabled.
Relevant Material Preview
This brings me to another thought. File snippets can mean loads of different things for different files. For this reason, applications can define ways to render snippets. Rendering can be in the form of text, rich text, images or even other applications' output. Why other applications' output? It's lame if the OS is in charge of things such as all the video playback with codecs galore ever changing. No, that makes the OS monolithic and breaks precious programming patterns. Of course one would aim on shipping the OS with a default video player, but I digress. By letting other applications render things for you, this enables third parties to customize snippet behavior without modifying the application itself. Say you have a text document that normally renders the text around what's found as relevant in its own way. Say the default behavior is the output the rich text, but you want it to output normal text. Assuming the application doesn't allow you to specify this yourself, there is a third party app that does this, and only this. Assign it to render that file's type and presto! Customization is at your fingertips.
Now I'm getting into just features the search application would provide. Granted there are craploads of ways to present information, but I won't go into those details now.
Replacing Explorer
What I want to talk about now is the user interface of the desktop manager. I've never really liked the taskbar and the start menu. The start menu has basically a directory hierarchy with links to files or applications that installed apps have deemed themselves worthy of adding to. This is clutter that becomes unnecessary with search. Screw the start menu. It's gone.
What do I LIKE about the start menu? Recent programs and access to control panel, along with links to the mostly used folders. But... what makes those folders so important? What criteria is used for determining which recently used apps are shown? This seems like customizable queries should be allowed. I actually don't like how recent programs messes up a lot and adds things I really don't want shown. This is another application where machine learning or AI could really show its shine. As for folders, ya... folders no longer exist. Only tags and relevancy by content. So what do we do? We show some default set of "popular tags'" query results along with some other logic we deem adds visibility weight. Obviously we can't/don't want to show all files tagged documents on the computer. No, we want to add importance like date made, times opened, etc. Really one could use tags to make a pseudo folder/file hierarchy, as I'm sure you can imagine, but that defeats the purpose of search, and isn't how people will think to organize. Say... you're loading pictures off your digital camera and normally would make a new folder in "Pictures\Jojo's family\Life in Madagascar" this time for "Summer 2008". This time, instead of navigating to Life in Madagascar and then making the file to import to, you're prompted to simply add tags. So "jojo's family Madagascar summer 2008" and pow, searches for jojo and more restricted searches will yield these pictures. For those who hate to type, search can be extended to finding relevant tags as well, so you can click through results and add tags to the list.
This need for metadata is the current major risk of the imaginary BrowserOS. I can see in the near future though, using facial recognition and other image processing, more indexing techniques can be added to the system to build tags to improve relevancy without the need for user input.
Feeds, Feeds, Feeds
Back to the desktop. Query results can be rendered in any control that is deemed capable of rendering data, even if not in the most verbose way (say of the search application). Controls can make up your desktop. Multiple desktops are also possible (think Spaces if you're a Mac fanboy, or Gnome/KDE if you're awesome and use linux) that are all customized different ways. When I visualize this, I think of iGoogle, and all the different feeds and widgets I can have everywhere. I also think of computers of tomorrow all on static IPs and server oriented, so you could set up queries to render RSS feeds and server iGoogle if you so wish. My aim is really to merge the internet and the desktop experience into one seemless vision.
Search could even show results from searching the local computer and with a search engine of choice. All these different modes would be easily discoverable in the search application.
Window Management
So yes, search result rendering, no more start menu, quick launch can be simple controls set up on the desktop that just fetch from a URI, but what of running applications? Surely those must be like windows and KDE and Gnome and Mac OSX somehow...? Nope. Running apps are just entries in the database as well. Granted, apps that start and stop all the time without showing themselves wouldn't be performing all these transactions in realtime. Applications will have execution tags that the desktop manager will be able to hook into. User apps, namely separate windows that normally show in the taskbar will have certain tags, background processes have other tags, but aren't added to the database until queried, or not at all. This information will likely just reside in memory. I imagine most likely that I would have alt-tab functionality only as a UI add-on that uses these queries. To actually show the gamut of applications running... I say default query in a feed somewhere. If an application needs to get your attention, the side of the screen could glow and once hovered over would show a feed of applications that are tagged to get your attention (think orange flashing tabs for a new AIM message for this attention-grabbing idea). Of course all this would be customizable as behavioral UI addons. Hell, an addon could actually show you the windows taskbar, if you really wanted it. In my opinion though, this is cluttered UI and won't be long missed once users get addicted to search.
Abstract
An amazing amount of our time is spent online. So much so that browsing the web has become more natural to us than browsing our computer. My vision of computers in the future (apart from Minority Report-style holographic and surface computing) involves intertwining the browser and the rest of the computer. What I see involves probably the biggest risk toward this approach, and that is getting rid of hierarchical directories to store files, but rather allowing a user to search for documents via a common search engine query.
The File System (BrowserFS)
Files can be tagged by users and also by a background data mining process for relevancy determining algorithms. The way to best implement this is to have one's hard drive be totally a one- to two-level database system.
What is a two-level database system? Well, in my mind there are three types of files. User-created/owned, executable, and application data. Application data would be stored in the second level of the database. The second level is a database as a blob entry in the first level of the database in order to minimize clutter and narrow query results to relevant areas. The motivation for this, or rather my inspiration for this comes from my observation of two classes of applications. One class uses many flat files in complex directory hierarchies, and the other uses very few "packed" files which are basically virtual file systems that have all those many flat files organized as described of the previous class. Obviously one approach is cleaner than the other, and there only exists one level of indirection between the two. If the OS API has a boolean in fopen, say, that specifies if the data is first or second level, the resulting query could be limited to the application database.
"But wait!" you say, "Applications don't need to search for their data files, since they know exactly what they need. Don't introduce this overhead." I agree 100%, which brings me to my next idea.
The development tools for this operating system would allow order to be introduced to files residing on the build system. A tool that could create directory hierarchies that references files residing on the system would output a necessary build file for dependent data files. We impose directory hierarchies because hey, we know that's how we organize without ad hoc search queries. The most important reason however is because creating a URI to the file would allow direct access without queries. Since before shipping an application, one generally works in debug mode, debug applications would use this hierarchy file to open the referenced files on the first level database. Ship applications however would compile the second level database BLOB and work as described.
Applications can still access all other files; first or second level. The second level database is just another file in the first level database, only access to it is optimized more in the OS kernel. Thus if a user specifies he wants to use that application database file that a search has given him, he can, and then browse though that database as well. This is all if he has the permissions to do so, of course.
So where are the first level files, and how do applications access them once search spits them out? Well they all have URIs too, and querying the database in standard fashion can output all files on your computer if one so desires. The main difference is that first-level file URIs are assigned by the OS, and the second-level file URIs are assigned by the developer.
File Name and Extension Makeover
File names and file extensions are no longer what you might think either. A file extension is an attribute of a file record in the database that will either reference an application (applications register extensions with the OS by simply being applications on the system) that will open it, or are generic (ex. type EXT) and do not reference an application. So developers can still change a file's type, and it's still by changing what filename.end ends with, but by changing the extension, a disambiguation text extension would ask if it's for common applications A, B, C, Generic, or search. With machine learning, the OS can determine the behavior it should take by default for changing certain file names to others.
Keep in mind file names are no longer file names. They're optional titles that are also part of the user tags (weighted differently though) that are displayed on search results, along with snippets, if enabled.
Relevant Material Preview
This brings me to another thought. File snippets can mean loads of different things for different files. For this reason, applications can define ways to render snippets. Rendering can be in the form of text, rich text, images or even other applications' output. Why other applications' output? It's lame if the OS is in charge of things such as all the video playback with codecs galore ever changing. No, that makes the OS monolithic and breaks precious programming patterns. Of course one would aim on shipping the OS with a default video player, but I digress. By letting other applications render things for you, this enables third parties to customize snippet behavior without modifying the application itself. Say you have a text document that normally renders the text around what's found as relevant in its own way. Say the default behavior is the output the rich text, but you want it to output normal text. Assuming the application doesn't allow you to specify this yourself, there is a third party app that does this, and only this. Assign it to render that file's type and presto! Customization is at your fingertips.
Now I'm getting into just features the search application would provide. Granted there are craploads of ways to present information, but I won't go into those details now.
Replacing Explorer
What I want to talk about now is the user interface of the desktop manager. I've never really liked the taskbar and the start menu. The start menu has basically a directory hierarchy with links to files or applications that installed apps have deemed themselves worthy of adding to. This is clutter that becomes unnecessary with search. Screw the start menu. It's gone.
What do I LIKE about the start menu? Recent programs and access to control panel, along with links to the mostly used folders. But... what makes those folders so important? What criteria is used for determining which recently used apps are shown? This seems like customizable queries should be allowed. I actually don't like how recent programs messes up a lot and adds things I really don't want shown. This is another application where machine learning or AI could really show its shine. As for folders, ya... folders no longer exist. Only tags and relevancy by content. So what do we do? We show some default set of "popular tags'" query results along with some other logic we deem adds visibility weight. Obviously we can't/don't want to show all files tagged documents on the computer. No, we want to add importance like date made, times opened, etc. Really one could use tags to make a pseudo folder/file hierarchy, as I'm sure you can imagine, but that defeats the purpose of search, and isn't how people will think to organize. Say... you're loading pictures off your digital camera and normally would make a new folder in "Pictures\Jojo's family\Life in Madagascar" this time for "Summer 2008". This time, instead of navigating to Life in Madagascar and then making the file to import to, you're prompted to simply add tags. So "jojo's family Madagascar summer 2008" and pow, searches for jojo and more restricted searches will yield these pictures. For those who hate to type, search can be extended to finding relevant tags as well, so you can click through results and add tags to the list.
This need for metadata is the current major risk of the imaginary BrowserOS. I can see in the near future though, using facial recognition and other image processing, more indexing techniques can be added to the system to build tags to improve relevancy without the need for user input.
Feeds, Feeds, Feeds
Back to the desktop. Query results can be rendered in any control that is deemed capable of rendering data, even if not in the most verbose way (say of the search application). Controls can make up your desktop. Multiple desktops are also possible (think Spaces if you're a Mac fanboy, or Gnome/KDE if you're awesome and use linux) that are all customized different ways. When I visualize this, I think of iGoogle, and all the different feeds and widgets I can have everywhere. I also think of computers of tomorrow all on static IPs and server oriented, so you could set up queries to render RSS feeds and server iGoogle if you so wish. My aim is really to merge the internet and the desktop experience into one seemless vision.
Search could even show results from searching the local computer and with a search engine of choice. All these different modes would be easily discoverable in the search application.
Window Management
So yes, search result rendering, no more start menu, quick launch can be simple controls set up on the desktop that just fetch from a URI, but what of running applications? Surely those must be like windows and KDE and Gnome and Mac OSX somehow...? Nope. Running apps are just entries in the database as well. Granted, apps that start and stop all the time without showing themselves wouldn't be performing all these transactions in realtime. Applications will have execution tags that the desktop manager will be able to hook into. User apps, namely separate windows that normally show in the taskbar will have certain tags, background processes have other tags, but aren't added to the database until queried, or not at all. This information will likely just reside in memory. I imagine most likely that I would have alt-tab functionality only as a UI add-on that uses these queries. To actually show the gamut of applications running... I say default query in a feed somewhere. If an application needs to get your attention, the side of the screen could glow and once hovered over would show a feed of applications that are tagged to get your attention (think orange flashing tabs for a new AIM message for this attention-grabbing idea). Of course all this would be customizable as behavioral UI addons. Hell, an addon could actually show you the windows taskbar, if you really wanted it. In my opinion though, this is cluttered UI and won't be long missed once users get addicted to search.
Sunday, July 20, 2008
Unstructured Thoughts on Structures
As an undergraduate in mathematics, I know more math than you, but still less math than epsilon. It is for this reason that most all my opinions and thoughts on mathematics are much more romantic than they are useful. I have written papers on different areas that interested me, and I have gone to many different talks and read several papers. Could I come up with an hypothesis and prove it? Probably not, but given my current position in university, I am sure I could find guidance toward starting such an endeavor.
My goal with this blog is to increase readers' interest in mathematics and programming. I plan on talking about many random topics (but not truly random... a very fun investigation to do right there) that come to catch my interest, and I also aim to post solutions to different programming problems I come across. As long as my solutions to obscure problems are archived on the net, search engines will be able to index them and help a programmer in distress in the future.
I plan not to touch such topics as politics, philosophy or my personal life, but as an opinionated person without the motivation to maintain more than one blog, I make no promises about the future.
Back to the topic of this post, "Unstructured Thoughts on Structures." I am sure by now you have observed the unstructured thoughts, but what of these structures? Mathematics is all about creating abstractions to quantitatively and generally describe a problem. Structures, namely algebraic structures, are currently my focus of interest. Group theory, ring theory, field theory and Galois theory may ring bells for some of you. This is what I am talking about. This area of mathematics is so vastly different from anything else one studies before it that even mathematicians like to joke about it not being, "real math." A quote comes to mind from a source I cannot currently recall that is along the lines of, "Now we can solve this problem without any math at all; just group theory!" With this tidbit about structures to pique your interest, I will save more depth descriptions and discussions for later posts.
Welcome to my blog, friends of mathematics and computers.
My goal with this blog is to increase readers' interest in mathematics and programming. I plan on talking about many random topics (but not truly random... a very fun investigation to do right there) that come to catch my interest, and I also aim to post solutions to different programming problems I come across. As long as my solutions to obscure problems are archived on the net, search engines will be able to index them and help a programmer in distress in the future.
I plan not to touch such topics as politics, philosophy or my personal life, but as an opinionated person without the motivation to maintain more than one blog, I make no promises about the future.
Back to the topic of this post, "Unstructured Thoughts on Structures." I am sure by now you have observed the unstructured thoughts, but what of these structures? Mathematics is all about creating abstractions to quantitatively and generally describe a problem. Structures, namely algebraic structures, are currently my focus of interest. Group theory, ring theory, field theory and Galois theory may ring bells for some of you. This is what I am talking about. This area of mathematics is so vastly different from anything else one studies before it that even mathematicians like to joke about it not being, "real math." A quote comes to mind from a source I cannot currently recall that is along the lines of, "Now we can solve this problem without any math at all; just group theory!" With this tidbit about structures to pique your interest, I will save more depth descriptions and discussions for later posts.
Welcome to my blog, friends of mathematics and computers.
Subscribe to:
Posts (Atom)