The intersection inference problem is NP-complete

PDF for this post
First let me start off by defining the intersection inference problem.

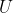
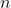
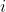
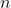
Given a set , some finite number () subsets , and constants , is there a subset such that for ranging all values?

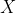
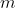
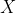
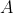
First we prove that intersection inference is in NP. Suppose we have a solution . In order to verify that is indeed a solution, we perform the intersections of with and confirm that . Set intersection can be performed (naively) in time, so this process is indeed polynomial and clearly yields the correct answer. Thus intersection inference is in NP.

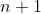
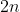
To prove intersection inference is NP-complete, we will show a reduction from 3-dimensional mapping to the intersection inference problem. With an arbitrary instance of the 3-dimensional mapping problem defined as sets such that , and . To reduce this to the intersection inference problem, let , and define to be the subsets of triples that contain respectively. Define in a similar manner from to for and from to for . Finally define . The constraints are and for . 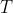We can see that to create these subsets takes time in the rather straightforward manner of iterating over 's elements to divvy up the elements into arrays representing .

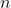
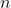
Through this construction we can see that exactly triples must match, and only one triple can contain each specific element in . Thus if there exists a solution to this intersection inference problem, the solution is exactly the triples that satisfy the 3-dimensional matching problem. If there does not exist a solution, then at least one constraint was not satisfied, meaning at least one element in was not covered, or all elements were covered with some redundancies. Thus the reduction is correct and intersection inference is NP-complete because a known NP-complete problem was poly-time reducible to the intersection inference problem which is in NP.